長方形の周の長さ
今日は太郎くんのクラスで長方形の周の長さに関する問題について考えているようです。 さてどんな問題なんでしょうか。
先生
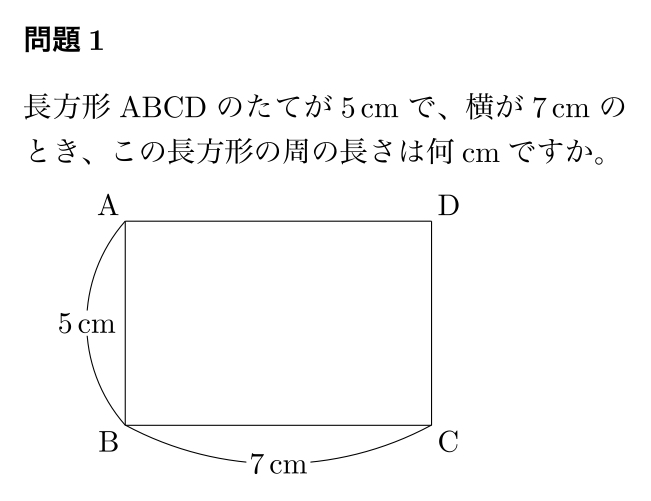
「さあみんな、この問題を解いてみよう。ただし、計算回数はなるべく少なくすること。」
太郎
「これは僕にまかせて。長方形の周ってことは、ぐるっと一周の長さってことですよね。 だったら、5+7+5+7だから、えっと、5+7が12で、12+5が17で、17+7が24。 24cmだあ。」
花子
「太郎くんは3回計算したわね。じゃあ私は、たてが2つで5×2=10。横が2つで7×2=14。全部合わせて、10+14で24。 太郎くんと同じ答えだ。計算したのも3回。これ以上少なくするのは無理なんじゃないかな。」
先生
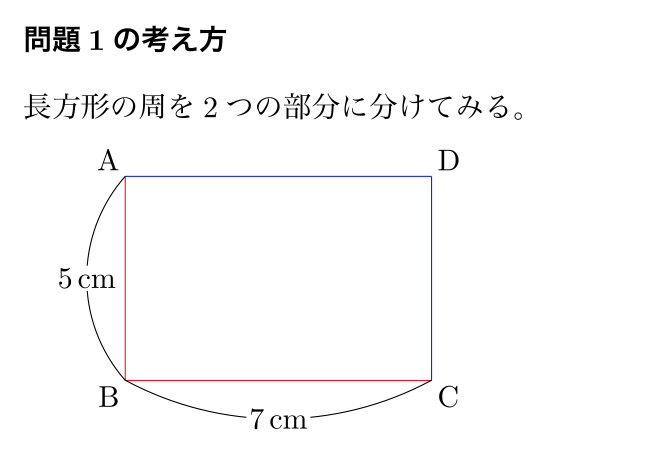
「ふふふ、どうかな。こんな風に考えてみてはどうだろうか。 長方形の周を2つの部分に分けて、それぞれ赤と青で色をつけてみよう。」
先生
「赤いところだけ、つまりたて1つと横1つで何cmになるかな。」
太郎
「5+7で12cmです。」
花子
「青いところも12cm。ってことは、周の長さは12×2で24cmだわ。2回計算しただけで答えが出ちゃった。」
先生
「そう、2回でできるんだね。では、まとめておこう。」
先生
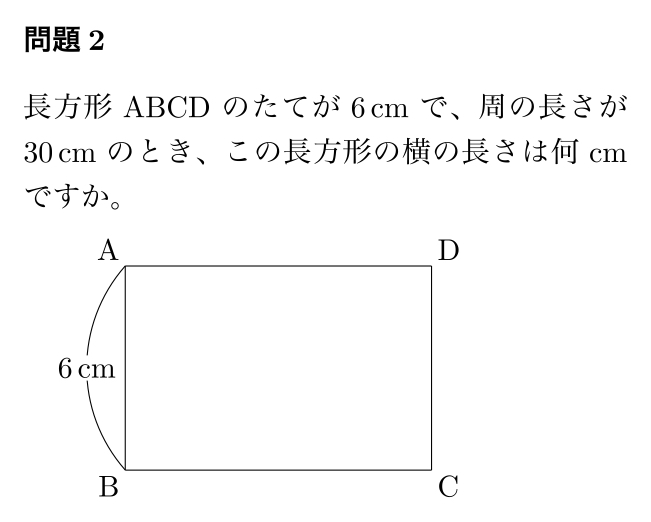
「では、もう一問いってみよう。」
太郎
「今度こそ僕にまかせて。周の長さが30cmだから、（たて+横）は30÷2で15cmです。 たては6cmだから、横は15-6で9cmです。」
先生
「いいぞ太郎くん、大正解だ。前の問題で学んだことをうまく活用できたね。素晴らしい。」
花子
「太郎くん、なかなかやるわね。次のテストでも正解できるようによく復習しとかないとね。」
太郎
「余裕っす。」
意外に苦手な人が多い、長方形の周の長さの応用問題
長方形の周の長さを求めるのは、ほとんどの生徒が簡単にできてしまいます。 一方で、まわりとたての長さから横の長さを求める問題は、なかなか手がつけられない生徒が多いのも事実です。 テストのときには、これが応用問題として出題されるかもしれません。 そのときは太郎くんたちのやり取りを思い出してください。